Gaussian Network Model (GNM)¶
This example shows how to perform GNM calculations using an X-ray structure
of ubiquitin. A GNM instance that stores the Kirchhoff matrix and
normal mode data describing the intrinsic dynamics of the protein structure
will be obtained. GNM instances and individual normal modes
(Mode) can be used as input to functions in prody.dynamics
module.
See [Bahar97] and [Haliloglu97] for more information on the theory of GNM.
| [Bahar97] | Bahar I, Atilgan AR, Erman B. Direct evaluation of thermal fluctuations in protein using a single parameter harmonic potential. Folding & Design 1997 2:173-181. |
| [Haliloglu97] | Haliloglu T, Bahar I, Erman B. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 1997 79:3090-3093. |
Parse structure¶
We start by importing everything from the ProDy package:
In [1]: from prody import *
In [2]: from matplotlib.pylab import *
In [3]: ion() # turn interactive mode on
First we parse a PDB file by passing its identifier to
parsePDB() function. Note that if file is not found in
the current working directory, it will be downloaded.
In [4]: ubi = parsePDB('1aar')
In [5]: ubi
Out[5]: <AtomGroup: 1aar (1218 atoms)>
This file contains 2 chains, and a flexible C-terminal (residues 71-76). We only want to use Cα atoms of first 70 residues from chain A, so we select them:
In [6]: calphas = ubi.select('calpha and chain A and resnum < 71')
In [7]: calphas
Out[7]: <Selection: 'calpha and chai...and resnum < 71' from 1aar (70 atoms)>
See definition of “calpha”, “chain”, and other selection keywords in Atom Selections.
Note that, flexible design of classes allows users to select atoms other than alpha carbons to be used in GNM calculations.
Build Kirchhoff matrix¶
Instantiate a GNM instance:
In [8]: gnm = GNM('Ubiquitin')
We can build Kirchhoff matrix using selected atoms and
GNM.buildKirchhoff() method:
In [9]: gnm.buildKirchhoff(calphas)
We can get a copy of the Kirchhoff matrix using GNM.getKirchhoff()
method:
In [10]: gnm.getKirchhoff()
Out[10]:
array([[11., -1., -1., ..., 0., 0., 0.],
[-1., 15., -1., ..., 0., 0., 0.],
[-1., -1., 20., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., 20., -1., -1.],
[ 0., 0., 0., ..., -1., 21., -1.],
[ 0., 0., 0., ..., -1., -1., 12.]])
Parameters¶
We didn’t pass any parameters, but GNM.buildKirchhoff() method accepts
two of them, which by default are cutoff=10.0 and gamma=1.0, i.e.
buildKirchhoff(calphas, cutoff=10., gamma=1.)
In [11]: gnm.getCutoff()
Out[11]: 10.0
In [12]: gnm.getGamma()
Out[12]: 1.0
Note that it is also possible to use an externally calculated Kirchhoff matrix.
Just pass it to the GNM instance using GNM.setKirchhoff() method.
Calculate normal modes¶
We now calculate normal modes from the Kirchhoff matrix.
In [13]: gnm.calcModes()
Note that by default 20 non-zero (or non-trivial) modes and 1 trivial mode are
calculated. Trivial modes are not retained. To calculate different numbers
of non-zero modes or to keep zero modes, try gnm.calcModes(50, zeros=True).
Normal mode data¶
Get eigenvalues and eigenvectors:
In [14]: gnm.getEigvals().round(3)
Out[14]:
array([ 2.502, 2.812, 4.366, 5.05 , 7.184, 7.65 , 7.877, 9.08 ,
9.713, 10.132, 10.502, 10.644, 10.888, 11.157, 11.285, 11.632,
11.78 , 11.936, 12.006, 12.218])
In [15]: gnm.getEigvecs().round(3)
Out[15]:
array([[-0.064, -0.131, -0.245, ..., -0.256, 0.538, -0. ],
[-0.073, -0.085, -0.19 , ..., 0.006, -0.069, 0.032],
[-0.076, -0.043, -0.135, ..., 0.017, -0.047, 0.018],
...,
[-0.092, 0.064, 0.105, ..., 0.032, -0.042, 0.006],
[-0.07 , 0.099, 0.054, ..., 0.031, 0.024, -0.014],
[-0.081, 0.135, 0.124, ..., 0.013, -0.04 , -0.018]])
Get covariance matrix:
In [16]: gnm.getCovariance().round(2)
Out[16]:
array([[ 0.08, 0.02, 0.01, ..., -0.01, -0.01, -0.01],
[ 0.02, 0.02, 0.01, ..., -0. , -0. , -0.01],
[ 0.01, 0.01, 0.01, ..., 0. , -0. , -0. ],
...,
[-0.01, -0. , 0. , ..., 0.01, 0.01, 0.01],
[-0.01, -0. , -0. , ..., 0.01, 0.01, 0.02],
[-0.01, -0.01, -0. , ..., 0.01, 0.02, 0.05]])
Note that covariance matrices are calculated using the available modes in the model, which is the slowest 20 modes in this case. If the user calculates M modes, these M modes will be used in calculating the covariance matrix.
Individual modes¶
Normal mode indices start from 0, so slowest mode has index 0.
In [17]: slowest_mode = gnm[0]
In [18]: slowest_mode.getEigval().round(3)
Out[18]: 2.502
In [19]: slowest_mode.getEigvec().round(3)
Out[19]:
array([-0.064, -0.073, -0.076, -0.112, -0.092, -0.143, -0.164, -0.205,
-0.24 , -0.313, -0.192, -0.152, -0.066, -0.07 , -0.025, -0.031,
0.001, -0.006, -0.015, 0.027, 0.042, 0.055, 0.063, 0.09 ,
0.09 , 0.069, 0.132, 0.175, 0.145, 0.121, 0.195, 0.218,
0.158, 0.217, 0.245, 0.214, 0.225, 0.171, 0.2 , 0.151,
0.102, 0.043, -0.029, -0.064, -0.072, -0.086, -0.09 , -0.078,
-0.057, -0.011, 0.016, 0.061, 0.058, 0.043, 0.029, 0.013,
0.004, 0.011, -0.013, -0.037, -0.05 , -0.059, -0.07 , -0.094,
-0.094, -0.099, -0.097, -0.092, -0.07 , -0.081])
By default, modes with 0 eigenvalue are excluded. If they were retained, slowest non-trivial mode would have index 6.
Access hinge sites¶
Hinge sites identified from all calculated modes (n_modes defined when
calling gnm.calcModes()) can be obtain by using the following command.
In [20]: hinges = calcHinges(gnm)
In [21]: hinges[:5]
Out[21]: [0, 1, 2, 3, 4]
Hinge sites in the slowest mode can be obtained by:
In [22]: calcHinges(gnm[0])
Out[22]: [16, 18, 42, 49, 57]
Hinge sites identified from multiple modes (e.g. 2 modes) can be accessed by:
In [23]: calcHinges(gnm[:2])
Out[23]: [3, 14, 16, 18, 25, 42, 43, 46, 47, 48, 49, 57, 65]
These numbers correspond to node indices in the GNM object, which does not know anything about the original atoms. In order to get the residue numbers corresponding to these hinges, we can index the resum array with the hinges list as follows:
In [24]: resnums = calphas.getResnums()
In [25]: mode2_hinges = calcHinges(gnm[1])
In [26]: resnums[mode2_hinges]
Out[26]: array([ 4, 15, 26, 44, 47, 48, 49, 66])
Plot results¶
ProDy plotting functions are prefixed with show. Let’s use some of them
to plot data:
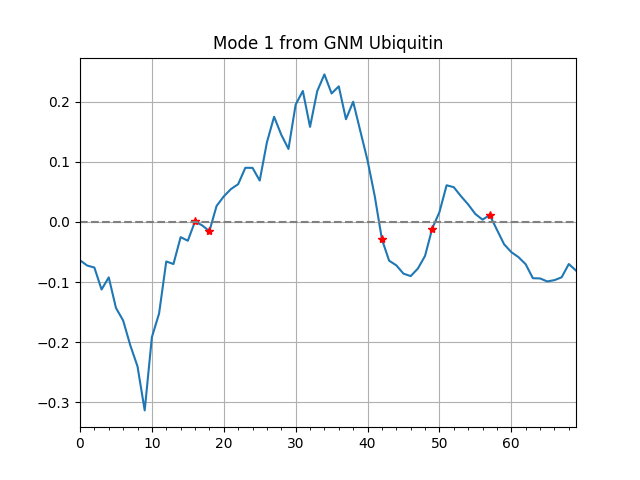
Slow mode shape¶
By default, hinge sites will be shown in mode shape plot indicated by
red stars, and it can be turned off by setting hinges=False.
The option zero=True is to turn on the reference line of zero.
In [29]: showMode(gnm[0], hinges=True, zero=True);
In [30]: grid();
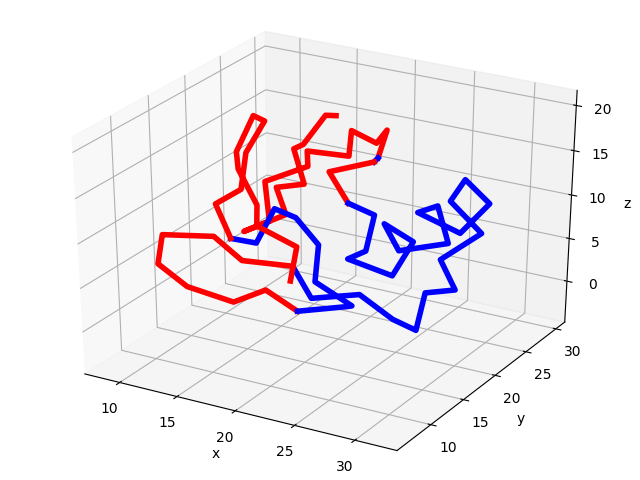
Protein structure bipartition¶
Given a GNM mode, protein structure can be partitioned into two parts that move
with respect to each other. The function showProtein() can take a GNM mode
as input and visualize the bipartition.
In [32]: showProtein(calphas, mode=gnm[0]);