Calculations

Here are the required imports again. You do not need to repeat them if you are still in the same python session.

In [1]: from prody import *

In [2]: from pylab import *

In [3]: ion()

Loading a structure and applying the anisotropic network model

First, we parse a structure that we want to analyse with PRS. For this tutorial, we will fetch the near-intact full length AMPAR structure 3kg2 from the PDB. We import a subset containing the calpha atoms, which we will use in downstream steps.

In [4]: ampar_ca = parsePDB('3kg2', subset='ca')

Next, create an ANM instance and calculate modes from which the covariance matrix can be calculated. We could ask for all modes rather than the default subset of the first 20 global modes. We could alternatively apply the PRS to another model from which a covariance matrix could be derived such as PCA, GNM or an MD simulation.

In [5]: anm_ampar = ANM('AMPAR 3kg2')

In [6]: anm_ampar.buildHessian(ampar_ca)

In [7]: anm_ampar.calcModes()

PRS can also be performed with any other model from which a covariance matrix can be calculated including GNM and PCA. A PCA model can also be used with an external covariance matrix using its PCA.setCovariance() method. ANM is used here to reproduce the published data.

Showing the PRS matrix with effectiveness and sensitivity profiles

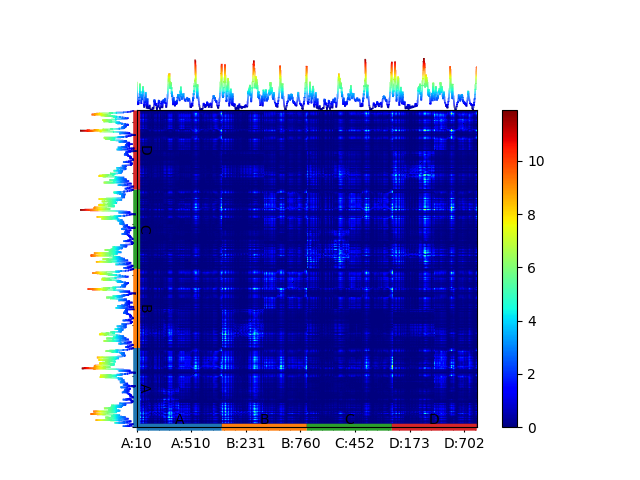
The PRS matrix is then calculated from the covariance matrix from the ANM of the AMPAR. This can be automatically carried out together with plotting using the following code. We supply atoms to allow us to delineate residue numbers and chains.

In [8]: show = showPerturbResponse(anm_ampar, atoms=ampar_ca)

In [9]: plt.show()

Saving the model

You can also save the ANM model in a .npz file for loading again and write an .nmd for visualizing in the NMWiz. Adding matrices=True allows us to save the covariance matrix so we can calculate the PRS faster in future analyses.

In [10]: saveModel(anm_ampar, '3kg2', matrices=True)
Out[10]: '3kg2.anm.npz'

In [11]: writeNMD('anm_3kg2.nmd', anm_ampar, ampar_ca)
Out[11]: 'anm_3kg2.nmd'

The next page illustrates some more detailed analyses.