Plotting

Synopsis

This example is continued from Analysis. The aim of this part is to produce graphical comparisons of experimental and theoretical data. We will reproduce the plots that was presented in our paper [AB09].

Load data

First, we load data saved in Calculations:

In [1]: from prody import *

In [2]: from pylab import *

In [3]: ion()

In [4]: pca = loadModel('p38_xray.pca.npz')

In [5]: anm = loadModel('1p38.anm.npz')

In [6]: ensemble = loadEnsemble('p38_X-ray.ens.npz')

In [7]: ref_chain = parsePDB('p38_ref_selection.pdb')

PCA - ANM overlap

In previous page, we compared PCA and ANM modes to get some numbers. In this case, we will use plotting functions to make similar comparisons:

In [8]: showOverlapTable(pca[:6], anm[:6]);

# Let's change the title of the figure
In [9]: title('PCA - ANM Overlap Table');
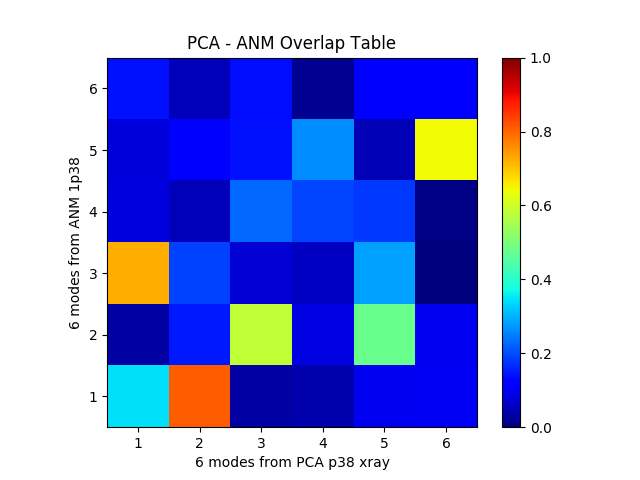
../../_images/ensemble_analysis_xray_overlap_table.png

It is also possible to plot overlap of a single mode from one model with multiple modes from another:

In [10]: showOverlap(pca[0], anm);
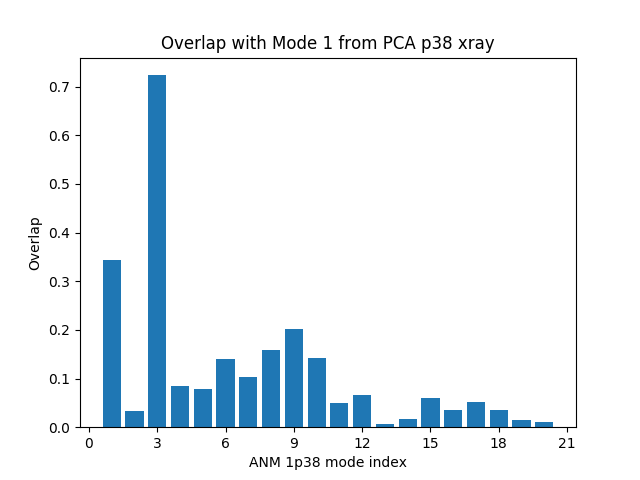
../../_images/ensemble_analysis_xray_overlap.png

Let’s also plot the cumulative overlap in the same figure:

In [11]: showOverlap(pca[0], anm);

In [12]: showCumulOverlap(pca[0], anm, 'r');
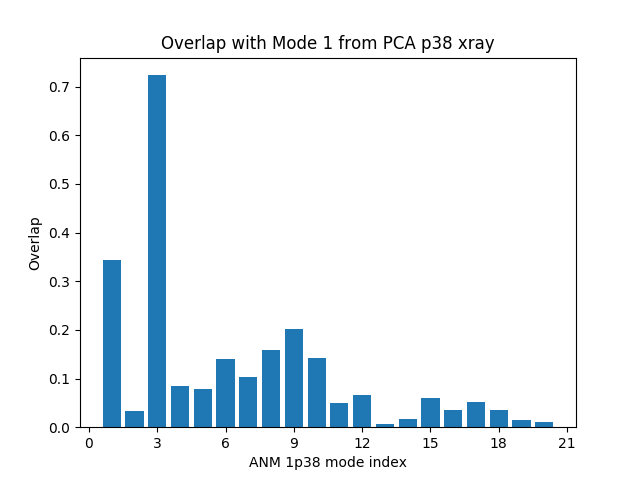
../../_images/ensemble_analysis_xray_cumulative_overlap.png

Square fluctuations

In [13]: showSqFlucts(pca[:3]);

In [14]: showSqFlucts(anm[:3]);
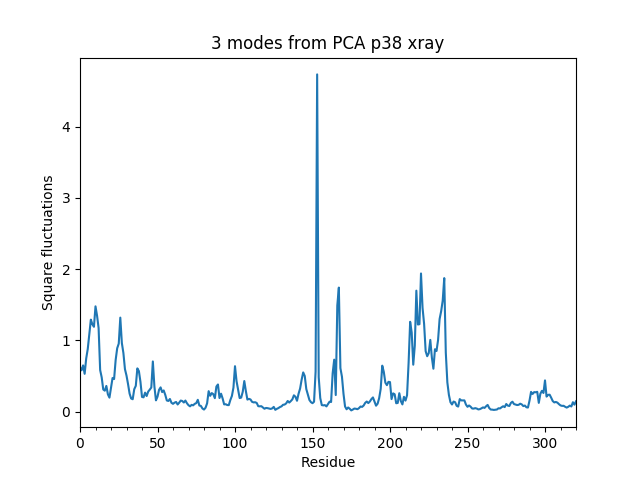
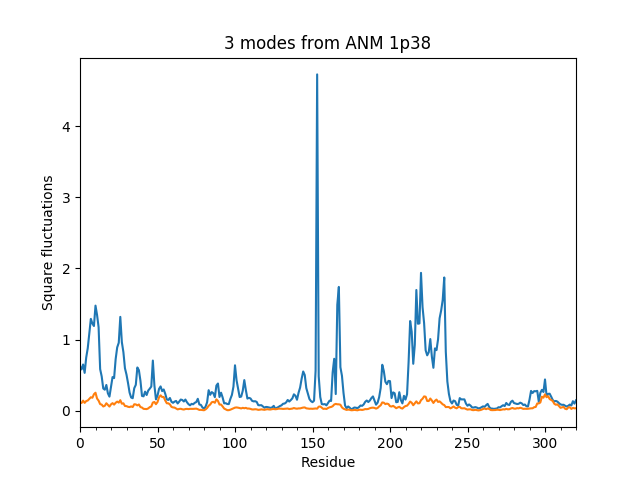
../../_images/ensemble_analysis_xray_pca_sqflucts.png ../../_images/ensemble_analysis_xray_anm_sqflucts.png

Now let’s plot square fluctuations along PCA and ANM modes in the same plot:

In [15]: showScaledSqFlucts(pca[0], anm[2]);

In [16]: legend();
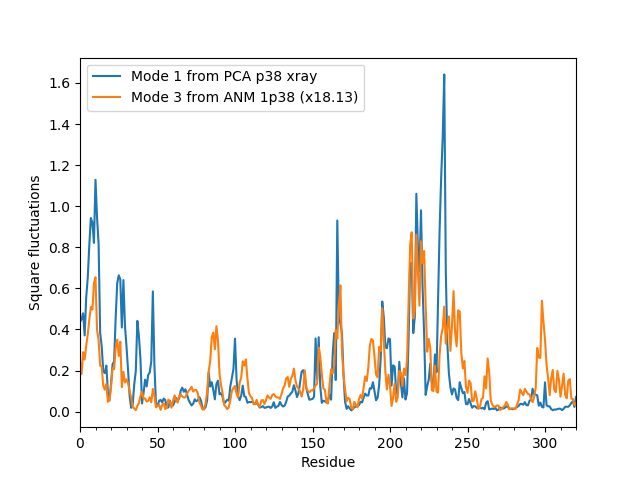
../../_images/ensemble_analysis_xray_pca_anm_sqflucts_1.png 
In [17]: showScaledSqFlucts(pca[1], anm[0]);

In [18]: legend();
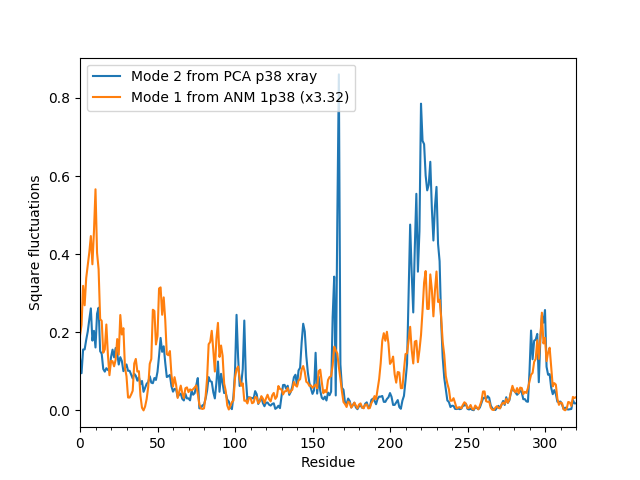
../../_images/ensemble_analysis_xray_pca_anm_sqflucts_2.png

In the above example, ANM modes are scaled to have the same mean as PCA modes. Alternatively, we could plot normalized square fluctuations:

In [19]: showNormedSqFlucts(pca[0], anm[2]);

In [20]: legend();
../../_images/ensemble_analysis_xray_pca_anm_sqflucts_3.png

Projections

Now we will project the ensemble onto PC 1 and 2 using showProjection():

In [21]: showProjection(ensemble, pca[:2]);

In [22]: axis([-0.8, 0.8, -0.8, 0.8]);
../../_images/ensemble_analysis_xray_pca_projection.png

Now we will do a little more work, and get a colorful picture:

red unbound
blue inhibitor bound
yellow glucoside bound
purple peptide/protein bound 
In [23]: color_list = ['red', 'blue', 'blue', 'blue', 'blue', 'blue', 'blue', 'blue',
   ....:               'blue', 'purple', 'purple', 'blue', 'blue', 'blue',
   ....:               'blue', 'blue', 'red', 'red', 'red', 'blue', 'blue',
   ....:               'blue', 'blue', 'blue','blue', 'blue', 'blue', 'blue',
   ....:               'blue', 'red', 'blue', 'blue','blue', 'blue', 'blue',
   ....:               'blue', 'blue', 'blue', 'blue', 'blue', 'blue', 'yellow',
   ....:               'yellow', 'yellow', 'yellow', 'blue', 'blue','blue',
   ....:               'blue', 'blue', 'blue', 'yellow', 'purple', 'purple',
   ....:               'blue', 'yellow', 'yellow', 'yellow', 'blue', 'yellow',
   ....:               'yellow', 'blue', 'blue', 'blue', 'blue', 'blue', 'blue',
   ....:               'blue', 'blue', 'blue', 'blue', 'blue', 'blue', 'blue',
   ....:               'blue', 'blue', 'blue', 'purple']
   ....: 

In [24]: color2label = {'red': 'Unbound', 'blue': 'Inhibitor bound',
   ....:                'yellow': 'Glucoside bound',
   ....:                'purple': 'Peptide/protein bound'}
   ....: 

In [25]: label_list = [color2label[color] for color in color_list]

In [26]: showProjection(ensemble, pca[:2], color=color_list,
   ....:                label=label_list);
   ....: 

In [27]: axis([-0.8, 0.8, -0.8, 0.8]);

In [28]: legend();
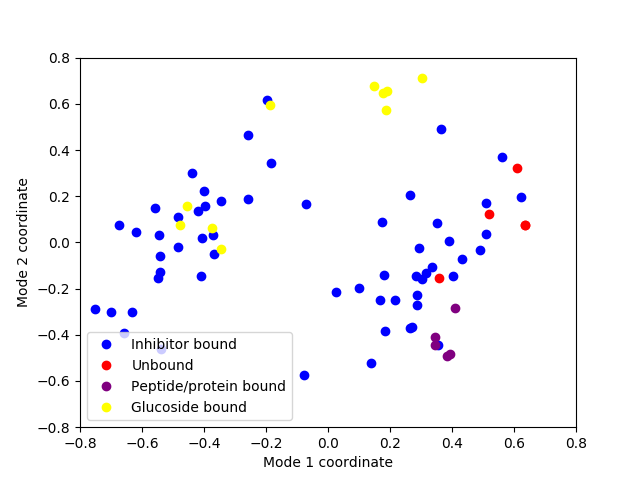
../../_images/ensemble_analysis_xray_pca_projection_2.png

Now let’s project conformations onto 3d principal space and label conformations using text keyword argument and PDBEnsemble.getLabels() method:

In [29]: showProjection(ensemble, pca[:3], color=color_list, label=label_list,
   ....:                text=ensemble.getLabels(), fontsize=10);
   ....:
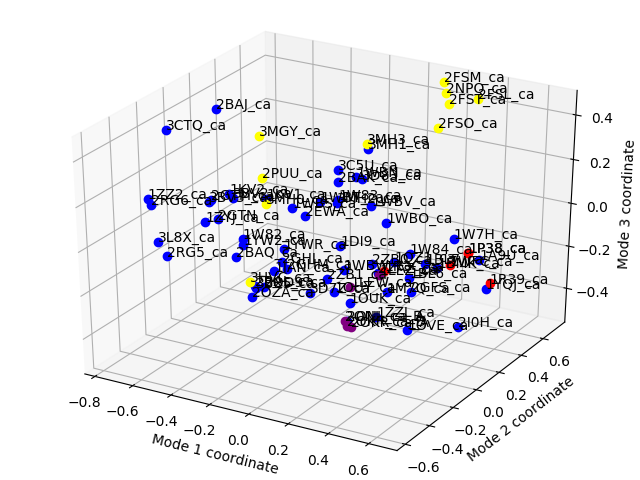
../../_images/ensemble_analysis_xray_pca_projection_3.png

The figure with all conformation labels is crowded, but in an interactive session you can zoom in and out to make text readable.

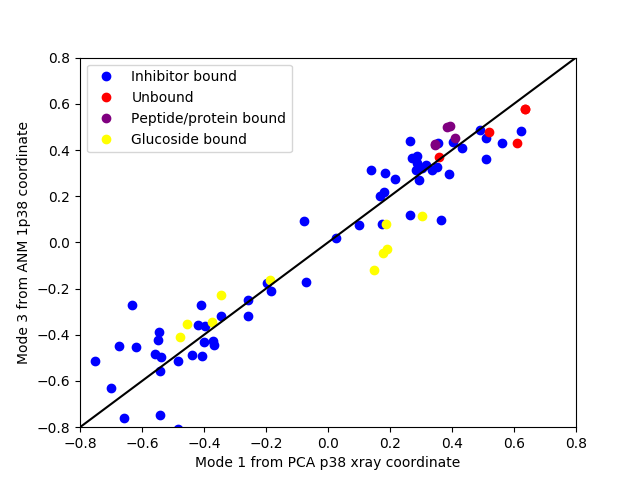
Cross-projections

Finally, we will make a cross-projection plot comparing PCA modes and ANM modes using showCrossProjection(). We will pass the scale='y' argument, which will scale the width of the projection along the ANM mode:

In [30]: showCrossProjection(ensemble, pca[0], anm[2], scale="y",
   ....:                      color=color_list, label=label_list);
   ....: 

In [31]: plot([-0.8, 0.8], [-0.8, 0.8], 'k');

In [32]: axis([-0.8, 0.8, -0.8, 0.8]);

In [33]: legend(loc='upper left');
../../_images/ensemble_analysis_xray_cross_projection_1.png 
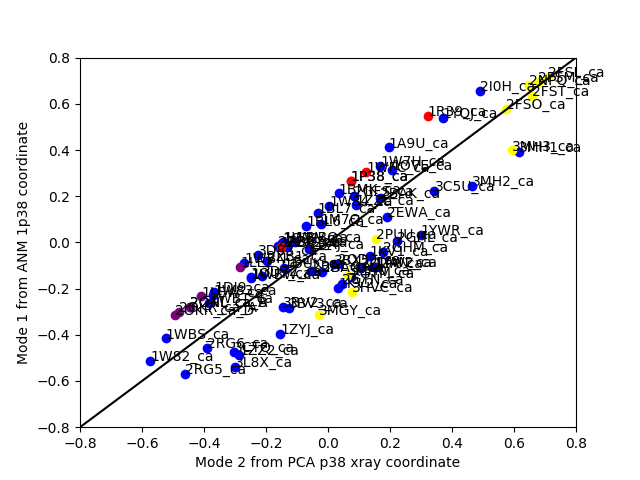
In [34]: showCrossProjection(ensemble, pca[1], anm[0], scale="y",
   ....:                     color=color_list, label=label_list);
   ....: 

In [35]: plot([-0.8, 0.8], [-0.8, 0.8], 'k');

In [36]: axis([-0.8, 0.8, -0.8, 0.8]);
../../_images/ensemble_analysis_xray_cross_projection_2.png

It is also possible to find the correlation between these projections:

In [37]: pca_coords, anm_coords = calcCrossProjection(ensemble, pca[0], anm[2])

In [38]: print(np.corrcoef(pca_coords, anm_coords))
[[ 1.         -0.95443933]
 [-0.95443933  1.        ]]

This shows 0.95 for the PC 1 and ANM mode 2 pair.

Finally, it is also possible to label conformations in cross projection plots too:

In [39]: showCrossProjection(ensemble, pca[1], anm[0], scale="y",
   ....:     color=color_list, label=label_list, text=ensemble.getLabels(),
   ....:     fontsize=10);
   ....: 

In [40]: plot([-0.8, 0.8], [-0.8, 0.8], 'k');

In [41]: axis([-0.8, 0.8, -0.8, 0.8]);
../../_images/ensemble_analysis_xray_cross_projection_2.png