Custom Gamma Functions

This example shows how to develop custom force constant functions for ANM (or GNM) calculations.

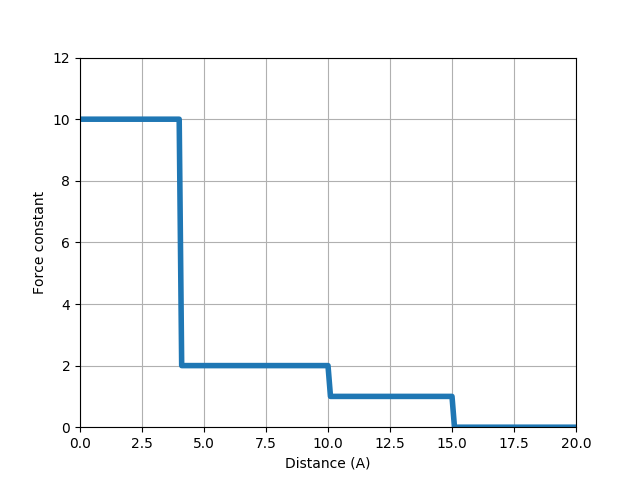
We will use the relation shown in the figure below. For Cα atoms that are 10 to 15 Å apart from each other, we use a unit force constant. For those that are 4 to 10 Å apart, we use a 2 times stronger force constant. For those that are within 4 Å of each other (i.e. those from connected residue pairs), we use a 10 times stronger force constant.

We will obtain an ANM instance that stores Hessian and Kirchhoff matrices and normal mode data describing the intrinsic dynamics of the protein structure. ANM instances and individual normal modes (Mode) can be used as input to functions in prody.dynamics module.

Parse structure

We start by importing everything from ProDy, NumPy, and Matplotlib packages:

In [1]: from prody import *

In [2]: from matplotlib.pylab import *

In [3]: ion() # turn interactive mode on

We start with parsing a PDB file by passing an identifier.

In [4]: p38 = parsePDB('1p38')

In [5]: p38
Out[5]: <AtomGroup: 1p38 (2962 atoms)>

We want to use only Cα atoms, so we select them:

In [6]: calphas = p38.select('protein and name CA')

In [7]: calphas
Out[7]: <Selection: 'protein and name CA' from 1p38 (351 atoms)>

Force Constant Function

We define the aformentioned function as follows:

In [8]: def gammaDistanceDependent(dist2, *args):
   ...:     """Return a force constant based on the given square distance."""
   ...:     if dist2 <= 16:
   ...:         return 10
   ...:     elif dist2 <= 100:
   ...:         return 2
   ...:     elif dist2 <= 225:
   ...:         return 1
   ...:     else:
   ...:         return 0
   ...: 

Note that the input to this function from ANM or GNM is the square of the distance. In addition, node (atom or residue) indices are passed to this function, that’s why we used *args in the function definition.

Let’s test how it works:

In [9]: dist = arange(0, 20, 0.1)

In [10]: gamma = map(gammaDistanceDependent, dist ** 2)

In [11]: plot(dist, gamma, lw=4);

In [12]: axis([0, 20, 0, 12]);

In [13]: xlabel('Distance (A)');

In [14]: ylabel('Force constant');

In [15]: grid();

ANM calculations

We use selected atoms (351 Cα’s) and gammaDistanceDependent function for ANM calculations as follows:

In [16]: anm = ANM('1p38')

In [17]: anm.buildHessian(calphas, cutoff=15, gamma=gammaDistanceDependent)

In [18]: anm.calcModes()

For more detailed examples see Anisotropic Network Model (ANM) or Gaussian Network Model (GNM).