Sequence-Structure Comparison¶
The part shows how to compare sequence conservation properties with structural mobility obtained from Gaussian network model (GNM) calculations.
In [1]: from prody import *
In [2]: from matplotlib.pylab import *
In [3]: ion() # turn interactive mode on
Entropy Calculation¶
First, we retrieve MSA for protein for protein family PF00074:
In [4]: fetchPfamMSA('PF00074')
Out[4]: 'PF00074_full.sth'
We parse the MSA file:
In [5]: msa = parseMSA('PF00074_full.sth')
Then, we refine it using refineMSA() based on the sequence of
RNAS1_BOVIN:
In [6]: msa_refine = refineMSA(msa, label='RNAS1_BOVIN', seqid=0.98)
We calculate the entropy for the refined MSA:
In [7]: entropy = calcShannonEntropy(msa_refine)
Mobility Calculation¶
Next, we obtain residue fluctuations or mobility for protein member of the above family. We will use chain B of 2W5I.
In [8]: pdb = parsePDB('2W5I', chain='B')
We can use the function alignSequenceToMSA() to identify the part of
the PDB file that matches with the MSA. In cases where this fails, a label
keyword argument can be provided to the function as well.
In [9]: aln, idx_1, idx_2 = alignSequenceToMSA(pdb, msa_refine, label='RNAS1_BOVIN')
In [10]: showAlignment(aln, indices=[idx_1, idx_2])
20 30 40 50 60
2W5IB KETAAAKFERQHMDSSTSAASSSNYCNQMMKSRNLTKDRCKPVNTFVHESLADVQAVCSQ
18 28 38 48 58
RNAS1_BOVIN --TAAAKFERQHMDSSTSAASSSNYCNQMMKSRNLTKDRCKPVNTFVHESLADVQAVCSQ
70 80 90 100 110 120
2W5IB KNVACKNGQTNCYQSYSTMSITDCRETGSSKYPNCAYKTTQANKHIIVACEGNPYVPVHF
68 78 88 98 108 118
RNAS1_BOVIN KNVACKNGQTNCYQSYSTMSITDCRETGSSKYPNCAYKTTQANKHIIVACEGNPYVPVHF
2W5IB DASV
RNAS1_BOVIN D---
This tells us that the first two residues are missing as are the last three, ending the sequence at residue 121. Hence, we make a selection accordingly:
In [11]: chB = pdb.select('resnum 3 to 121')
We can see from the sequence that this gives us the right portion:
In [12]: chB.ca.getSequence()
Out[12]: 'TAAAKFERQHMDSSTSAASSSNYCNQMMKSRNLTKDRCKPVNTFVHESLADVQAVCSQKNVACKNGQTNCYQSYSTMSITDCRETGSSKYPNCAYKTTQANKHIIVACEGNPYVPVHFD'
We write this selection to a PDB file for use later, e.g. with evol apps.
In [13]: writePDB('2W5IB_3-121.pdb', chB)
Out[13]: '2W5IB_3-121.pdb'
We perform GNM as follows:
In [14]: gnm = GNM('2W5I')
In [15]: gnm.buildKirchhoff(chB.ca)
In [16]: gnm.calcModes(n_modes=None) # calculate all modes
Now, let’s obtain residue mobility using the slowest mode, the slowest 8 modes, and all modes:
In [17]: mobility_1 = calcSqFlucts(gnm[0])
In [18]: mobility_1to8 = calcSqFlucts(gnm[:8])
In [19]: mobility_all = calcSqFlucts(gnm[:])
See Gaussian Network Model (GNM) for details.
Comparison of mobility and conservation¶
We use the above data to compare structural mobility and degree of conservation. We can calculate a correlation coefficient between the two quantities:
In [20]: result = corrcoef(mobility_all, entropy)
In [21]: result.round(3)[0,1]
Out[21]: 0.396
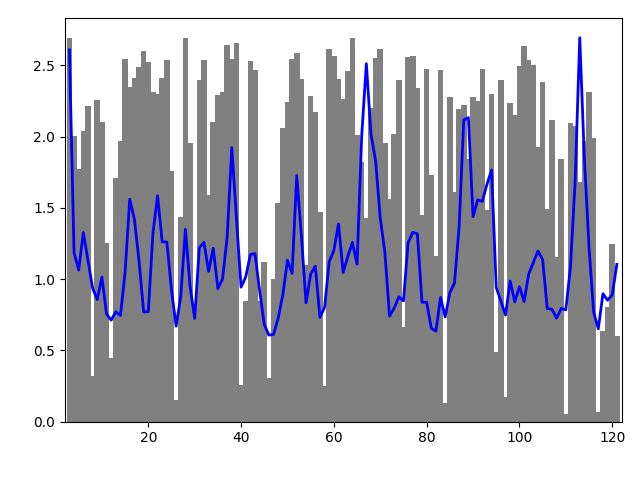
We can plot the two curves simultaneously to visualize the correlation. We have to scale the values of mobility to display them in the same plot.
Plotting¶
In [22]: indices = chB.ca.getResnums()
In [23]: bar(indices, entropy, width=1.2, color='grey');
In [24]: xlim(min(indices)-1, max(indices)+1);
In [25]: plot(indices, mobility_all*(max(entropy)/max(mobility_all)), color='b',
....: linewidth=2);
....:
Writing PDB files¶
We can also write PDB with b-factor column replaced by entropy and mobility values respectively. We can then load the PDB structure in VMD or PyMol to see the distribution of entropy and mobility on the structure.
In [26]: selprot = chB.copy()
In [27]: resindex = selprot.getResindices()
In [28]: entropy_prot = [entropy[ind] for ind in resindex]
In [29]: mobility_prot = [mobility_all[ind]*10 for ind in resindex]
In [30]: selprot.setBetas(entropy_prot)
In [31]: writePDB('2W5I_entropy.pdb', selprot)
Out[31]: '2W5I_entropy.pdb'
In [32]: selprot.setBetas(mobility_prot)
In [33]: writePDB('2W5I_mobility.pdb', selprot)
Out[33]: '2W5I_mobility.pdb'
We can see on the structure just as we could in the bar graph that there is some correlation with highly conserved (low entropy) regions having low mobility and high entropy regions have higher mobility.
