Core Calculations¶
In order to infer signature dynamics features we create mode ensembles from the
PDB ensembles by calculating normal modes for each member of the
PDBEnsemble as in the previous page or [SZ18].
First, make necessary imports from ProDy and Matplotlib packages if you haven’t already.
In [1]: from prody import *
In [2]: from pylab import *
In [3]: ion()
Mode Ensemble¶
For this analysis we’ll use the PDBEnsemble object,
which we just created, to build a ModeEnsemble.
There are options to select the model (GNM by default) and the way of
considering non-aligned residues (default is reduceModel(), which treats
them as environment).
If necessary, we first load the ensemble:
In [4]: ens = loadEnsemble('LeuT.ens.npz')
Then we calculated first 20 GNM modes for each member of the ensemble:
In [5]: gnms = calcEnsembleENMs(ens, model=GNM, trim='reduce', n_modes=20, match=True)
In [6]: gnms
Out[6]: <ModeEnsemble: 103 modesets (20 modes, 510 atoms)>
In this way, we will obtain one ModeSet for each member and 85 in total.
Finding a consistent order of modes across different mode sets is critical to the
accuracy of SignDy calculations. Therefore, in the above code, match is set
to True so that all other ModeSet`s are sorted to match the order of
the reference :class:.ModeSet`, which is the first ModeSet in the
ModeEnsemble by default.
Signature Dynamics¶
Signature dynamics are calculated as the mean and standard deviation of various properties such as mode shapes and mean square fluctations.
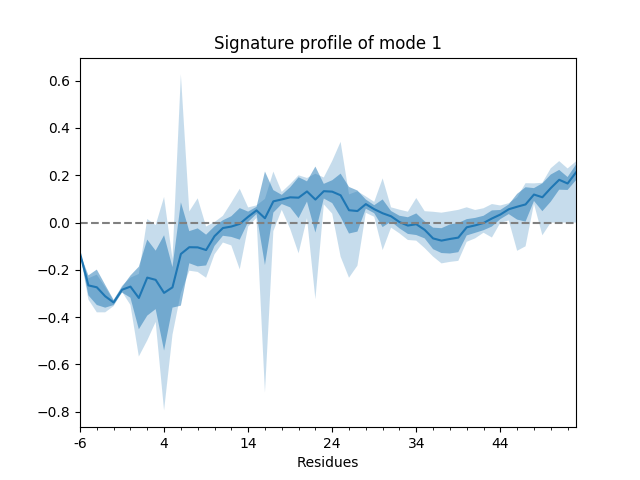
For example, we can show the average and standard deviation of the shape of the first mode (second index 0). The first index of the mode ensemble is over conformations.
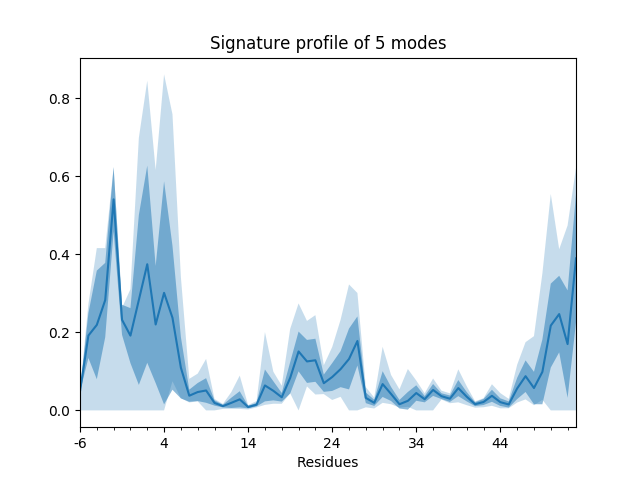
In the plot, the curve shows the mean values, the darker shade shows the standard deviations, and the lighter shade shows the range (minimum and maximum values). We can also show such things for properties involving multiple modes such as the mean square fluctuations from the first 5 modes,
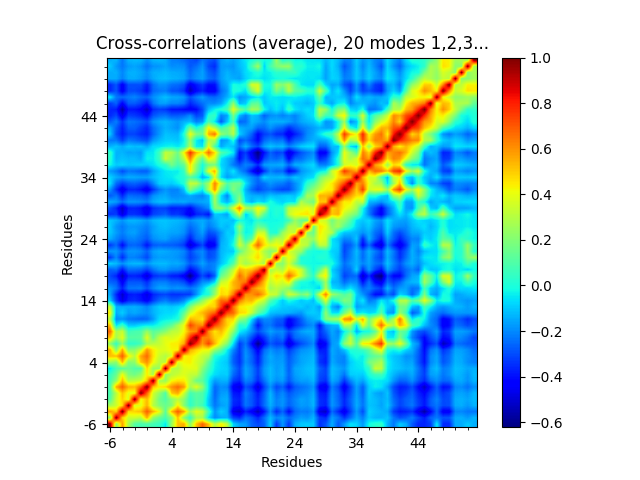
or the cross-correlations from the first 20.
We can also look at distributions over values across different members of the ensemble such as inverse eigenvalue. We can show a bar above this with individual members labelled like [JK15].
In [10]: highlights = {'2A65A': 'LeuT:OF', '3TT1A': 'LeuT:OF', ....: '3TT3A': 'LeuT:IF', '4US4A': 'MhsT:IF', ....: '3NCYA': 'AdiC:OF', '2X79A': 'Mhp1:IF', ....: '2WITA':'BetP', '4M48A':'DAT'} ....: In [11]: gs = plt.GridSpec(ncols=1, nrows=2, height_ratios=[1, 10], hspace=0.15) In [12]: subplot(gs[0]) Out[12]: <matplotlib.axes._subplots.AxesSubplot at 0x7fb4fb774210> In [13]: showVarianceBar(gnms[:, :5], fraction=True, highlights=highlights) Out[13]: ([<matplotlib.collections.PolyCollection at 0x7fb4fe38acd0>, <matplotlib.collections.PolyCollection at 0x7fb4fe38af90>, <matplotlib.collections.PolyCollection at 0x7fb4fe3ac250>, <matplotlib.collections.PolyCollection at 0x7fb4fe3ac510>, <matplotlib.collections.PolyCollection at 0x7fb4fe3ac7d0>, <matplotlib.collections.PolyCollection at 0x7fb4fe3acad0>, <matplotlib.collections.PolyCollection at 0x7fb4fe3acdd0>, <matplotlib.collections.PolyCollection at 0x7fb4fe351090>, <matplotlib.collections.PolyCollection at 0x7fb4fe351350>, <matplotlib.collections.PolyCollection at 0x7fb4fe351610>, <matplotlib.collections.PolyCollection at 0x7fb4fe3518d0>, <matplotlib.collections.PolyCollection at 0x7fb4fe351b90>, <matplotlib.collections.PolyCollection at 0x7fb4fe351ed0>, <matplotlib.collections.PolyCollection at 0x7fb4fe362190>, <matplotlib.collections.PolyCollection at 0x7fb4fe362450>, <matplotlib.collections.PolyCollection at 0x7fb4fe362710>, <matplotlib.collections.PolyCollection at 0x7fb4fe3629d0>, <matplotlib.collections.PolyCollection at 0x7fb4fe362d10>, <matplotlib.collections.PolyCollection at 0x7fb4fe362fd0>, <matplotlib.collections.PolyCollection at 0x7fb4fe385290>, <matplotlib.collections.PolyCollection at 0x7fb4fe385690>, <matplotlib.collections.PolyCollection at 0x7fb4fe385950>, <matplotlib.collections.PolyCollection at 0x7fb4fe385c10>, <matplotlib.collections.PolyCollection at 0x7fb4fe385ed0>, <matplotlib.collections.PolyCollection at 0x7fb4fe3271d0>, <matplotlib.collections.PolyCollection at 0x7fb4fe327490>, <matplotlib.collections.PolyCollection at 0x7fb4fe327750>, <matplotlib.collections.PolyCollection at 0x7fb4fe327a10>, <matplotlib.collections.PolyCollection at 0x7fb4fe327cd0>, <matplotlib.collections.PolyCollection at 0x7fb4fe327f90>, <matplotlib.collections.PolyCollection at 0x7fb4fe2dc250>, <matplotlib.collections.PolyCollection at 0x7fb4fe2dc590>, <matplotlib.collections.PolyCollection at 0x7fb4fe2dc850>, <matplotlib.collections.PolyCollection at 0x7fb4fe2dcb10>, <matplotlib.collections.PolyCollection at 0x7fb4fe2dce50>, <matplotlib.collections.PolyCollection at 0x7fb4fe2ee0d0>, <matplotlib.collections.PolyCollection at 0x7fb4fe2ee390>, <matplotlib.collections.PolyCollection at 0x7fb4fe2ee750>, <matplotlib.collections.PolyCollection at 0x7fb4fe2eea90>, <matplotlib.collections.PolyCollection at 0x7fb4fe2eedd0>, <matplotlib.collections.PolyCollection at 0x7fb4fe2ee990>, <matplotlib.collections.PolyCollection at 0x7fb4fe2a2290>, <matplotlib.collections.PolyCollection at 0x7fb4fe2a2550>, <matplotlib.collections.PolyCollection at 0x7fb4fe2a2890>, <matplotlib.collections.PolyCollection at 0x7fb4fe2a2b50>, <matplotlib.collections.PolyCollection at 0x7fb4fe2a2e50>, <matplotlib.collections.PolyCollection at 0x7fb4fe2b3190>, <matplotlib.collections.PolyCollection at 0x7fb4fe2b3510>, <matplotlib.collections.PolyCollection at 0x7fb4fe2b3810>, <matplotlib.collections.PolyCollection at 0x7fb4fe2b3b90>], [Text(0.538055,2.5,'LeuT:OF'), Text(0.452652,2.5,'MhsT:IF'), Text(0.532733,2.5,'DAT'), Text(0.464377,2.5,'AdiC:OF'), Text(0.494555,2.5,'LeuT:IF'), Text(0.499859,2.5,'LeuT:OF'), Text(0.504464,2.5,'BetP'), Text(0.531043,2.5,'Mhp1:IF')]) In [14]: xlabel('') Out[14]: Text(0.5,-7.27778,'') In [15]: subplot(gs[1]) Out[15]: <matplotlib.axes._subplots.AxesSubplot at 0x7fb4fe277d50> In [16]: showSignatureVariances(gnms[:, :5], fraction=True, bins=80, alpha=0.7) Out[16]: ([array([0. , 0.02912621, 0.00970874, 0.04854369, 0.02912621, 0.00970874, 0. , 0.01941748, 0.02912621, 0. , 0.01941748, 0.01941748, 0.11650485, 0.33009709, 0.16504854, 0.12621359, 0.01941748, 0.00970874, 0. , 0. , 0.00970874, 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]), array([0. , 0. , 0.02912621, 0.03883495, 0.00970874, 0. , 0. , 0. , 0. , 0. , 0.00970874, 0. , 0.00970874, 0. , 0.12621359, 0.02912621, 0.04854369, 0.15533981, 0.05825243, 0.01941748, 0.0776699 , 0.0776699 , 0.09708738, 0.02912621, 0. , 0.01941748, 0.03883495, 0.00970874, 0.01941748, 0.01941748, 0. , 0.01941748, 0.00970874, 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0.00970874, 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]), array([0.01941748, 0.05825243, 0.05825243, 0.00970874, 0.01941748, 0. , 0.01941748, 0. , 0.00970874, 0.00970874, 0.01941748, 0. , 0.00970874, 0. , 0. , 0.01941748, 0. , 0. , 0.00970874, 0.03883495, 0.02912621, 0. , 0.03883495, 0. , 0.06796117, 0.14563107, 0.02912621, 0.02912621, 0.03883495, 0.16504854, 0.12621359, 0.01941748, 0. , 0. , 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]), array([0.01941748, 0.06796117, 0.09708738, 0.03883495, 0.00970874, 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.02912621, 0.01941748, 0. , 0.00970874, 0. , 0.00970874, 0. , 0. , 0.00970874, 0.08737864, 0.00970874, 0. , 0.08737864, 0.04854369, 0.11650485, 0.08737864, 0.01941748, 0.06796117, 0.04854369, 0.01941748, 0.01941748, 0.01941748, 0.00970874, 0. , 0.01941748, 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.00970874, 0. , 0. ]), array([0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.00970874, 0. , 0. , 0. , 0. , 0. , 0.00970874, 0.01941748, 0.05825243, 0.15533981, 0.21359223, 0.0776699 , 0.10679612, 0.0776699 , 0.04854369, 0.03883495, 0.04854369, 0.05825243, 0.00970874, 0.02912621, 0.01941748, 0. , 0. , 0. , 0. , 0.00970874, 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ])], array([0.0143067 , 0.01779564, 0.02128458, 0.02477352, 0.02826245, 0.03175139, 0.03524033, 0.03872927, 0.0422182 , 0.04570714, 0.04919608, 0.05268502, 0.05617396, 0.05966289, 0.06315183, 0.06664077, 0.07012971, 0.07361865, 0.07710758, 0.08059652, 0.08408546, 0.0875744 , 0.09106334, 0.09455227, 0.09804121, 0.10153015, 0.10501909, 0.10850803, 0.11199696, 0.1154859 , 0.11897484, 0.12246378, 0.12595272, 0.12944165, 0.13293059, 0.13641953, 0.13990847, 0.14339741, 0.14688634, 0.15037528, 0.15386422, 0.15735316, 0.1608421 , 0.16433103, 0.16781997, 0.17130891, 0.17479785, 0.17828679, 0.18177572, 0.18526466, 0.1887536 , 0.19224254, 0.19573148, 0.19922041, 0.20270935, 0.20619829, 0.20968723, 0.21317617, 0.2166651 , 0.22015404, 0.22364298, 0.22713192, 0.23062086, 0.23410979, 0.23759873, 0.24108767, 0.24457661, 0.24806555, 0.25155448, 0.25504342, 0.25853236, 0.2620213 , 0.26551024, 0.26899917, 0.27248811, 0.27597705, 0.27946599, 0.28295493, 0.28644386, 0.2899328 ]), <a list of 5 Lists of Patches objects>) In [17]: xlabel('Mode weight') Out[17]: Text(0.5,23.5222,'Mode weight')
Saving the ModeEnsemble¶
Finally we save the mode ensemble for later processing:
In [18]: saveModeEnsemble(gnms, 'LeuT')
Out[18]: 'LeuT.modeens.npz'